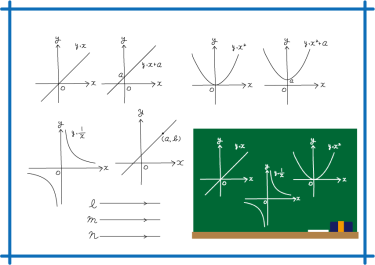
1関数とは何か?
関数は数学の中で重要な役割を果たす概念です。関数は入力と出力の対応関係を表し、ある値に対して別の値が対応する関係を表現します。例えば、数式「y = 2x + 3」は、xという値を入力するとそれに応じてyという値が出力される関数です。
2グラフを描くことの意味とは?
関数をグラフで表現することには大きな意味があります。グラフを描くことによって、関数の振る舞いや特徴を視覚的に理解することができます。直感的に関数の変化や傾向を把握することができ、数学的な概念を視覚化することでより具体的に捉えることができます。
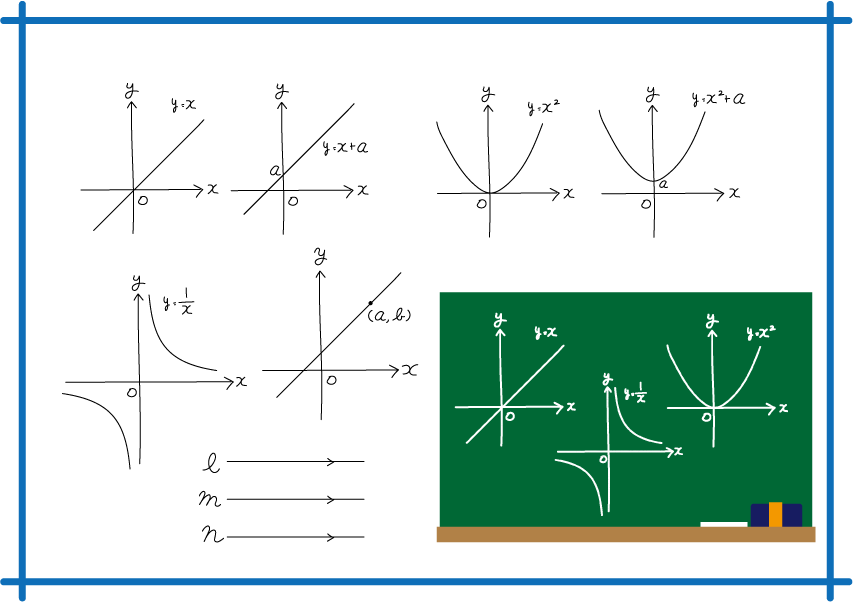
3関数の性質をグラフで読み解く
グラフを通じて関数の性質を読み解くことができます。例えば、関数が上に凸なのか下に凸なのか、増加傾向や減少傾向があるのかをグラフから判断することができます。また、関数が交点や極大値・極小値を持つ場合にも、グラフ上でその情報を視覚的に把握することができます。
4グラフが持つ情報と応用例
グラフはさまざまな情報を提供してくれます。関数の定義域や値域、増減の範囲、周期性など、関数の特性をグラフから読み取ることができます。また、実際の応用例としては、物理学や経済学、工学などの分野でグラフを用いて問題を解決したり、データを分析したりすることがあります。例えば、物体の運動を表す関数のグラフを使って、速度や加速度の変化を把握したり、経済の成長や変動をグラフで分析したりすることができます。
5グラフを描くための手法とツール
グラフを描くためにはいくつかの手法やツールがあります。まずは関数の式や特性を理解し、それを基にグラフを手書きで描く方法があります。また、数式処理ソフトやグラフ描画ソフトを使ってコンピュータ上でグラフを描くこともできます。さらに、オンラインのグラフ描画ツールやグラフ作成アプリも利用できます。それぞれの方法やツールには特徴や利点がありますので、使い方や選び方についても学んでおくと良いでしょう。
まとめ:
関数のグラフを描くことは、数学の概念を視覚化し、関数の性質や振る舞いをより具体的に理解するために重要です。グラフを通じて関数の増減傾向や特異点、周期性などを読み取ることができます。また、グラフを描くための手法やツールを使いこなすことで、より効率的にグラフを作成することができます。関数とグラフの組み合わせは、数学の世界をより鮮明にし、問題解決やデータ分析に役立ちます。ぜひ、関数とグラフの魅力を探求し、その重要性を実感してみてください!