数学の文字式の分野で覚えるべき公式のひとつに、分配法則というものがあります。
分配法則とは、a(b+c)=ab+acになるという公式のことで、これがないと文字式の分野は全く解けなくなる、といっても過言ではありません。それほど重要なものです。
しかし、これに分数が絡んだ問題は、一見解きにくく見えるかもしれません。
例えばこの問題を考えてみましょう。
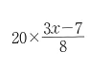
一見、20で全体をかけているように見えますが、この式において、(b+c)の中が何になるかを考えると、少し解きやすいかもしれません。
イメージできましたでしょうか?
この式の(b+c)にあたるものは、(3x-7)であり、aにあたるものは、20/8とも考えられます。もちろん、b+cを3x/8-7/8ととらえてもよいのですが、その方が計算の手間が増えるでしょう。
実際に、式全体をくくっているのが20/8の考え方を生徒さんに話したら、「じゃあ先に約分すればえやんな!?」といってくれました。
計算の手順を減らす良い工夫です、と一言で締めてもよいのですが、ここで大切なのはこれを自分で気づくことです。自分で気づいたものは、記憶に定着しやすい傾向にあると、心理学的にも証明されています。
様々なヒントを漏らさず、日々の気づきを大切にしていけるとよいですね。