この時期は、学校で扱っている範囲の関係上、中学生の生徒さんに比例や1次関数などのいわゆる「グラフ」についての範囲をお教えする機会が多くあります。
大人の目から見ると、一見、グラフの式に数字を当てはめれば終わりのように見えますが、この範囲の正答率は想像以上に低いです。この理由は何でしょうか。
何人かの生徒さんを見させていただいて、その理由は大きく2つに分けられることに気が付きました。
ひとつは、問題の意味が解らず、何をすればよいかわかっていないパターンで、初めて見る概念の理解が完璧でない場合に多く見られます。例えば、中学1年生比例の範囲を例にとると、ここだけでも「比例」「反比例」の周りに、「変数」「定数」「範囲」「座標」「軸」など、様々な言葉の意味をきちんと理解しなければ問題を解くための準備ができていない状態であるといえるでしょう。
このような生徒さんには、「その範囲」の知識の「前提」を理解することが優先されるといえます。
もうひとつは、そもそも計算そのものができていないパターンです。
それぞれ学年で、グラフの直前に扱う方程式の範囲は、長いうえに難しく、全ての学校の生徒が完璧にマスターして次の範囲に進められているかといわれると、完全には同意できません。
しかも、このような計算の範囲は、直後の範囲の正答率に直結します。
具体的な例として、1年生の方程式→比例・反比例の流れであれば「代入」や「(1次)方程式を解く」技能そのものが必要になり、2年生の連立方程式→1次関数の流れであれば交点を求めるのに連立方程式を使うことがよくあり、3年生の2次方程式→放物線では放物線そのものが2次方程式の式の形をしています。
つまり、その範囲以前の「前提」の知識をマスターしていないパターンがあるといえるでしょう。
私たち講師陣は、質問に来られた生徒さんがどこで詰まっていて、どこが苦手なのかを正確に把握し、一緒に問題を解決するお手伝いをさせていただいております。
特に後者の「計算そのもの」のパターンでは、どうしても時間がかかることもございますが、ひとつひとつできることを増やし、地力で解いていけるようにしていけるとよいですね。
ーーーーーーーーーーー
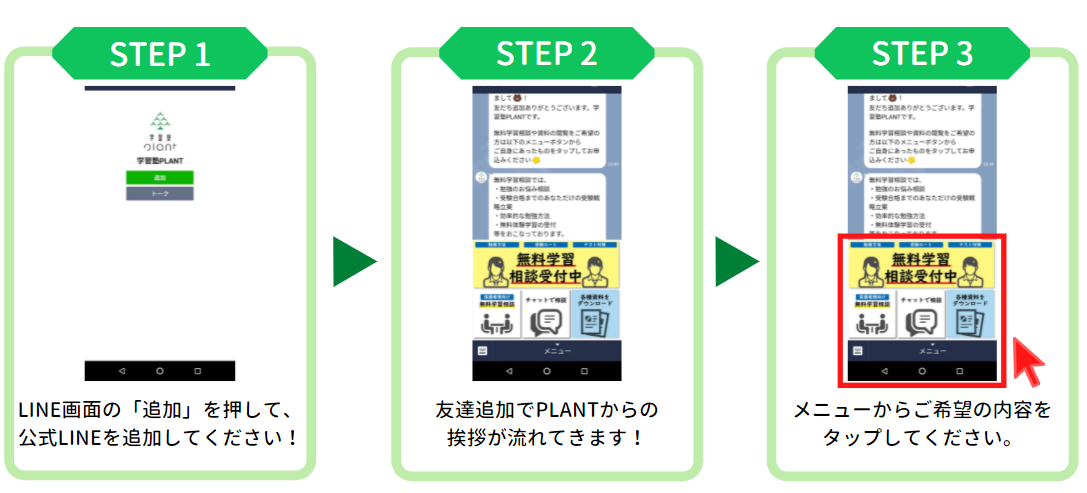
当塾の事が気になった方は
いつでもお気軽にお問合せください!
・近隣の小学校
西天満小学校・堀川小学校・開平小学校・滝川小学校・扇町小学校・桜宮小学校・追手門学院小学校・中大江小学校・中野小学校
・近隣の中学校
天満中学校・北稜中学校・東中学校・相愛中学校・追手門学院中学校・都島中学校
・近隣の高校
中央高校・大手前高校・相愛高校・星槎国際高校・扇町総合高校・東高校